Основные теоремы динамики системы материальных точек. Теоретическая механика
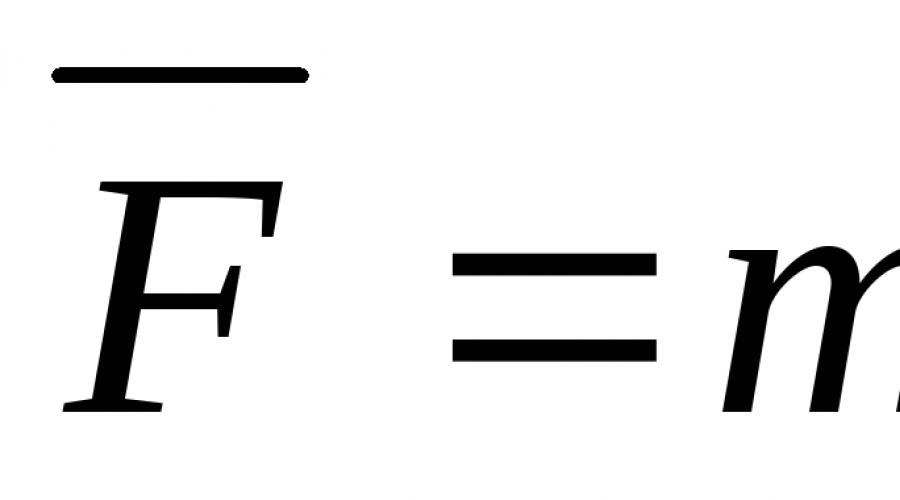
Читайте также
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Кубанский государственный технологический университет»
Теоретическая механика
Часть 2 динамика
Утверждено Редакционно-издательским
советом университета в качестве
Краснодар
УДК 531.1/3 (075)
Теоретическая механика. Часть 2. Динамика: Учебное пособие / Л.И.Драйко; Кубан. гос. технол.ун-т. Краснодар, 2011. 123 с.
ISBN 5-230-06865-5
Излагается в краткой форме теоретический материал, даны примеры решения задач, большинство из которых отражает реальные вопросы техники, уделено внимание выбору рационального способа решения.
Предназначено для бакалавров заочной и дистанционной форм обучения строительных, транспортных и машиностроительных направлений.
Табл. 1 Илл. 68 Библиогр. 20 назв.
Научный редактор канд.техн.наук,доц. В.Ф.Мельников
Рецензенты: зав.кафедрой теоретической механики и теории механизмов и машин Кубанского аграрного университета проф. Ф.М. Канарев; доцент кафедры теоретической механики Кубанского государственного технологического университета М.Е. Мултых
Печатается по решению Редакционно-издательского совета Кубанского государственного технологического университета.
Переиздание
ISBN 5-230-06865-5 КубГТУ 1998г.
Предисловие
Данное учебное пособие предназначено для студентов заочной формы обучения строительных, транспортных и машиностроительных специальностей, но может быть использовано при изучении раздела «Динамика» курса теоретической механики студентами заочниками других специальностей, а также студентами дневной формы обучения при самостоятельной работе.
Пособие составлено в соответствии с действующей программой курса теоретической механики, охватывает все вопросы основной части курса. Каждый раздел содержит краткий теоретический материал, снабженный иллюстрациями и методическими рекомендациями для его использования при решении задач. В пособии разобрано решение 30 задач, отражающих реальные вопросы техники и соответствующих контрольным заданиям для самостоятельного решения. Для каждой задачи представлена расчетная схема, наглядно иллюстрирующая решение. Оформление решения соответствует требованиям, предъявляемым к оформлению контрольных работ студентов-заочников.
Автор выражает глубокую признательность преподавателям кафедры теоретической механики и теории механизмов и машин Кубанского аграрного университета за большой труд по рецензированию учебного пособия, а также преподавателям кафедры теоретической механики Кубанского государственного технологического университета за ценные замечания и советы по подготовке учебного пособия к изданию.
Все критические замечания и пожелания будут приняты автором с благодарностью и в дальнейшем.
Введение
Динамика является наиболее важным разделом теоретической механики. Большинство конкретных задач, которые приходится в инженерной практике, относится к динамике. Используя выводы статики и кинематики, динамика устанавливает общие законы движения материальных тел под действием приложенных сил.
Простейшим материальным объектом является материальная точка. За материальную точку можно принять материальное тело любой формы, размерами которого в рассматриваемой задаче можно пренебречь. За материальную точку можно принимать тело конечных размеров, если различие в движении его точек для данной задачи не существенно. Это бывает в случае, когда размеры тела малы по сравнению с расстояниями, которые проходят точки тела. Каждую частицу твердого тела можно считать материальной точкой.
Силы, приложенные к точке или материальному телу, в динамике оцениваются по их динамическому воздействию, т. е. по тому, как они изменяют характеристики движения материальных объектов.
Движение материальных объектов с течением времени совершается в пространстве относительно определенной системы отсчета. В классической механике, опирающейся на аксиомы Ньютона, пространство считается трехмерным, его свойства не зависят от движущихся в нем материальных объектов. Положение точки в таком пространстве определяется тремя координатами. Время не связано с пространством и движением материальных объектов. Оно считается одинаковым для всех систем отсчета.
Законы динамики описывают движение материальных объектов по отношению к абсолютным осям координат, условно принятым за неподвижные. Начало абсолютной системы координат принимается в центре Солнца, а оси направляются на отдаленные, условно не подвижные звезды. При решении многих технических задач условно не подвижными можно считать координатные оси, связанные с Землей.
Параметры механического движения материальных объектов в динамике устанавливаются путем математических выводов из основных законов классической механики.
Первый закон (закон инерции):
Материальная точка сохраняет состояние покоя или равномерного и прямолинейного движения до тех пор, пока действие каких-либо сил не выведет ее из этого состояния.
Равномерное и прямолинейное движение точки называют движением по инерции. Покой является частным случаем движения по инерции, когда скорость точки равна нулю.
Всякая материальная точка обладает инертностью, т. е. стремится сохранить состояние покоя или равномерного прямолинейного движения. Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной, а движение, наблюдаемое по отношению к этой системе, называется абсолютным. Любая система отсчета, совершающая относительно инерциальной системы поступательное прямолинейное и равномерное движение, будет также инерциальной системой.
Второй закон (основной закон динамики):
Ускорение
материальной точки относительно
инерциальной системы отсчета
пропорционально приложенной к точке
силе и совпадает с силой по направлению:
 .
.
Из основного закона
динамики следует, что при силе
 ускорение
ускорение .
Масса точки характеризует степень
сопротивляемости точки изменению ее
скорости, т. е. является мерой инертности
материальной точки.
.
Масса точки характеризует степень
сопротивляемости точки изменению ее
скорости, т. е. является мерой инертности
материальной точки.
Третий закон (закон действия и противодействия):
Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены вдоль одной прямой в противоположные стороны.
Силы, именуемые действием и противодействием, приложены к разным телам и поэтому уравновешенной системы не образуют.
Четвертый закон (закон независимости действия сил):
При одновременном действии нескольких сил ускорение материальной точки равно геометрической сумме ускорений, которые имела бы точка при действии каждой силы в отдельности:
 , где
, где
 ,
, ,…,
,…, .
.
Общие теоремы динамики системы тел. Теоремы о движении центра масс, об изменении количества движения, об изменении главного момента количества движения, об изменении кинетической энергии. Принципы Даламбера, и возможных перемещений. Общее уравнение динамики. Уравнения Лагранжа.
Общие теоремы динамики твердого тела и системы тел
Общие теоремы динамики - это теорема о движении центра масс механической системы, теорема об изменении количества движения, теорема об изменении главного момента количества движения (кинетического момента) и теорема об изменении кинетической энергии механической системы.
Теорема о движении центра масс механической системы
Теорема о движении центра масс.
Произведение массы системы на ускорение ее центра масс равно векторной сумме всех действующих на систему внешних сил:
.
Здесь M
- масса системы:
;
a C
- ускорение центра масс системы:
;
v C
- скорость центра масс системы:
;
r C
- радиус вектор (координаты) центра масс системы:
;
- координаты (относительно неподвижного центра) и массы точек, из которых состоит система.
Теорема об изменении количества движения (импульса)
Количество движения (импульс) системы
равно произведению массы всей системы на скорость ее центра масс или сумме количества движения (сумме импульсов) отдельных точек или частей, составляющих систему:
.
Теорема об изменении количества движения в дифференциальной форме.
Производная по времени от количества движения (импульса) системы равна векторной сумме всех действующих на систему внешних сил:
.
Теорема об изменении количества движения в интегральной форме.
Изменение количества движения (импульса) системы за некоторый промежуток времени равно сумме импульсов внешних сил за тот же промежуток времени:
.
Закон сохранения количества движения (импульса).
Если сумма всех внешних сил, действующих на систему, равна нулю, то вектор количества движения системы будет постоянным. То есть все его проекции на оси координат будут сохранять постоянные значения.
Если сумма проекций внешних сил на какую либо ось равна нулю, то проекция количества движения системы на эту ось будет постоянной.
Теорема об изменении главного момента количества движения (теорема моментов)
Главным моментом количества движения системы относительно данного центра O
называется величина , равная векторной сумме моментов количеств движения всех точек системы относительно этого центра:
.
Здесь квадратные скобки обозначают векторное произведение.
Закрепленные системы
Следующая ниже теорема относится к случаю, когда механическая система имеет неподвижную точку или ось, которая закреплена относительно инерциальной системы отсчета. Например тело, закрепленное сферическим подшипником. Или система тел, совершающая движение вокруг неподвижного центра. Это также может быть неподвижная ось, вокруг которой вращается тело или система тел. В этом случае, под моментами следует понимать моменты импульса и сил относительно закрепленной оси.
Теорема об изменении главного момента количества движения (теорема моментов)
Производная по времени от главного момента количества движения системы относительно некоторого неподвижного центра O
равна сумме моментов всех внешних сил системы относительно того же центра.
Закон сохранения главного момента количества движения (момента импульса).
Если сумма моментов всех приложенных к системе внешних сил относительно данного неподвижного центра O
равна нулю, то главный момент количества движения системы относительно этого центра будет постоянным. То есть все его проекции на оси координат будут сохранять постоянные значения.
Если сумма моментов внешних сил относительно некоторой неподвижной оси равна нулю, то момент количества движения системы относительно этой оси будет постоянным.
Произвольные системы
Следующая далее теорема имеет универсальный характер. Она применима как к закрепленным системам, так и к свободно движущимся. В случае закрепленных систем нужно учитывать реакции связей в закрепленных точках. Она отличается от предыдущей теоремы тем, что вместо закрепленной точки O следует брать центр масс C системы.
Теорема моментов относительно центра масс
Производная по времени от главного момента количества движения системы относительно центра масс C
равна сумме моментов всех внешних сил системы относительно того же центра.
Закон сохранения момента импульса.
Если сумма моментов всех приложенных к системе внешних сил относительно центра масс C
равна нулю, то главный момент количества движения системы относительно этого центра будет постоянным. То есть все его проекции на оси координат будут сохранять постоянные значения.
Момент инерции тела
Если тело вращается вокруг оси z
с угловой скоростью ω z
,
то его момент количества движения (кинетический момент) относительно оси z
определяется по формуле:
L z = J z ω z
,
где J z
- момент инерции тела относительно оси z
.
Момент инерции тела относительно оси z
определяется по формуле:
,
где h k
- расстояние от точки массой m k
до оси z
.
Для тонкого кольца массы M
и радиуса R
или цилиндра, масса которого распределена по его ободу,
J z = M R 2
.
Для сплошного однородного кольца или цилиндра,
.
Теорема Штейнера-Гюйгенса.
Пусть Cz
- ось, проходящая через центр масс тела, Oz
- параллельная ей ось. Тогда моменты инерции тела относительно этих осей связаны соотношением:
J Oz = J Cz + M a 2
,
где M
- масса тела; a
- расстояние между осями.
В более общем случае
:
,
где - тензор инерции тела.
Здесь - вектор, проведенный из центра масс тела в точку с массой m k
.
Теорема об изменении кинетической энергии
Пусть тело массы M
совершает поступательное и вращательное движение с угловой скоростью ω
вокруг некоторой оси z
.
Тогда кинетическая энергия тела определяется по формуле:
,
где v C
- скорость движения центра масс тела;
J Cz
- момент инерции тела относительно оси, проходящей через центр масс тела параллельно оси вращения. Направление оси вращения может меняться со временем. Указанная формула дает мгновенное значение кинетической энергии.
Теорема об изменении кинетической энергии системы в дифференциальной форме.
Дифференциал (приращение) кинетической энергии системы при некотором ее перемещении равно сумме дифференциалов работ на этом перемещении всех приложенных к системе внешних и внутренних сил:
.
Теорема об изменении кинетической энергии системы в интегральной форме.
Изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил:
.
Работа, которую совершает сила
, равна скалярному произведению векторов силы и бесконечно малому перемещению точки ее приложения :
,
то есть произведению модулей векторов F
и ds
на косинус угла между ними.
Работа, которую совершает момент сил
, равна скалярному произведению векторов момента и бесконечно малого угла поворота :
.
Принцип Даламбера
Суть принципа Даламбера состоит в том, чтобы задачи динамики свести к задачам статики. Для этого предполагают (или это заранее известно), что тела системы имеют определенные (угловые) ускорения. Далее вводят силы инерции и (или) моменты сил инерции, которые равны по величине и обратные по направлению силам и моментам сил, которые по законам механики создавали бы заданные ускорения или угловые ускорения
Рассмотрим пример. Путь тело совершает поступательное движение и на него действуют внешние силы . Далее мы предполагаем, что эти силы создают ускорение центра масс системы . По теореме о движении центра масс, центр масс тела имел бы такое же ускорение, если бы на тело действовала сила . Далее мы вводим силу инерции:
.
После этого задача динамики:
.
;
.
Для вращательного движения поступают аналогичным образом. Пусть тело вращается вокруг оси z
и на него действуют внешние моменты сил M e zk
.
Мы предполагаем, что эти моменты создают угловое ускорение ε z
.
Далее мы вводим момент сил инерции M И = - J z ε z
.
После этого задача динамики:
.
Превращается в задачу статики:
;
.
Принцип возможных перемещений
Принцип возможных перемещений применяется для решений задач статики. В некоторых задачах, он дает более короткое решение, чем составление уравнений равновесия. Особенно это касается систем со связями (например, системы тел, соединенные нитями и блоками), состоящих из множества тел
Принцип возможных перемещений
.
Для равновесия механической системы с идеальными связями необходимо и достаточно, чтобы сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы была равна нулю.
Возможное перемещение системы - это малое перемещение, при котором не нарушаются связи, наложенные на систему.
Идеальные связи - это связи, которые не совершают работы при перемещении системы. Точнее, сумма работ, совершаемая самими связями при перемещении системы равна нулю.
Общее уравнение динамики (принцип Даламбера - Лагранжа)
Принцип Даламбера - Лагранжа - это объединение принцип Даламбера с принципом возможных перемещений. То есть, при решении задачи динамики, мы вводим силы инерции и сводим задачу к задаче статики, которую решаем с помощью принципа возможных перемещений.
Принцип Даламбера - Лагранжа
.
При движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и всех сил инерции на любом возможном перемещении системы равна нулю:
.
Это уравнение называют общим уравнением динамики
.
Уравнения Лагранжа
Обобщенные координаты q 1 , q 2 , ..., q n - это совокупность n величин, которые однозначно определяют положение системы.
Число обобщенных координат n совпадает с числом степеней свободы системы.
Обобщенные скорости - это производные от обобщенных координат по времени t .
Обобщенные силы Q 1
, Q 2
, ..., Q n
.
Рассмотрим возможное перемещение системы, при котором координата q k
получит перемещение δq k
.
Остальные координаты остаются неизменными. Пусть δA k
- это работа, совершаемая внешними силами при таком перемещении. Тогда
δA k = Q k δq k
,
или
.
Если, при возможном перемещении системы, изменяются все координаты, то работа, совершаемая внешними силами при таком перемещении, имеет вид:
δA = Q 1
δq 1
+ Q 2
δq 2
+ ... + Q n δq n
.
Тогда обобщенные силы являются частными производными от работы по перемещениям:
.
Для потенциальных сил
с потенциалом Π
,
.
Уравнения Лагранжа
- это уравнения движения механической системы в обобщенных координатах:
Здесь T
- кинетическая энергия. Она является функцией от обобщенных координат, скоростей и, возможно, времени. Поэтому ее частная производная также является функцией от обобщенных координат, скоростей и времени. Далее нужно учесть, что координаты и скорости являются функциями от времени. Поэтому для нахождения полной производной по времени нужно применить правило дифференцирования сложной функции:
.
Использованная литература:
С. М. Тарг, Краткий курс теоретической механики, «Высшая школа», 2010.
При большом количестве материальных точек, входящих в состав механической системы, или, если в её состав входят абсолютно твёрдые тела (), совершающие непоступательное движение, применение системы дифференциальных уравнений движения при решении основной задачи динамики механической системы оказывается практически неосуществимым. Однако при решении многих инженерных задач нет необходимости в определении движения каждой точки механической системы в отдельности. Иногда бывает достаточно сделать выводы о наиболее важных сторонах изучаемого процесса движения, не решая полностью систему уравнений движения. Эти выводы из дифференциальных уравнений движения механической системы составляют содержание общих теорем динамики. Общие теоремы, во-первых, освобождают от необходимости в каждом отдельном случае производить те математические преобразования, которые являются общими для разных задач и их раз и навсегда производят при выводе теорем из дифференциальных уравнений движения. Во-вторых, общие теоремы дают связь между общими агрегированными характеристиками движения механической системы, имеющими наглядный физический смысл. Эти общие характеристики, такие как количество движения, кинетический момент, кинетическая энергия механической системы называютсямерами движения механической системы.
Первая мера движения – количество движения механической системы
|
M k
|
Пусть
дана механическая система, состоящая
из
|
Количеством движения материальной точки называется векторная мера её движения, равная произведению массы точки на её скорость:
 .
.
Количеством движения механической системы называется векторная мера её движения, равная сумме количеств движения её точек:
 , (13.1)
, (13.1)
Преобразуем правую часть формулы (23.1):
где
 -
масса всей системы,
-
масса всей системы, -
скорость центра масс.
-
скорость центра масс.
Следовательно, количество движения механической системы равно количеству движения её центра масс, если сосредоточить в нём всю массу системы:
 .
.
Импульс силы
Произведение
силы на элементарный промежуток времени
её действия
 называется элементарным импульсом
силы.
называется элементарным импульсом
силы.
Импульсом
силы
 за промежуток времени
называется интеграл от элементарного
импульса силы
за промежуток времени
называется интеграл от элементарного
импульса силы
 .
.
Теорема об изменении количества движения механической системы
Пусть
на каждую точку
 механической
системы действуют равнодействующая
внешних сил
механической
системы действуют равнодействующая
внешних сил и равнодействующая внутренних сил
и равнодействующая внутренних сил .
.
Рассмотрим основные уравнения динамики механической системы
Складывая почленно уравнения (13.2) для n точек системы, получим
 (13.3)
(13.3)
Первая
сумма в правой части равна главному
вектору
 внешних сил системы. Вторая сумма равна
нулю по свойству внутренних сил системы.
Рассмотрим левую часть равенства (13.3):
внешних сил системы. Вторая сумма равна
нулю по свойству внутренних сил системы.
Рассмотрим левую часть равенства (13.3):
Таким образом, получим:
 , (13.4)
, (13.4)
или в проекциях на оси координат
 (13.5)
(13.5)
Равенства (13.4) и (13.5) выражают теорему об изменении количества движения механической системы:
Производная по времени от количества движения механической системы равна главному вектору всех внешних сил механической системы.
Эту теорему можно представить также в интегральной форме, проинтегрировав обе части равенства (13.4) по времени в пределах от t 0 до t :
 , (13.6)
, (13.6)
где
 ,
а интеграл в правой части – импульс
внешних сил за
,
а интеграл в правой части – импульс
внешних сил за
время t -t 0 .
Равенство (13.6) представляет теорему в интегральной форме:
Приращение количества движения механической системы за конечное время равно импульсу внешних сил за это время.
Теорему называют также теоремой импульсов.
В проекциях на оси координат, теорема запишется в виде:
Следствия (законы сохранения количества движения)
1).
Если главный вектор внешних сил за
рассматриваемый промежуток времени
равен нулю, то количество движения
механической системы постоянно, т.е.
если
 ,
, .
.
2). Если проекция главного вектора внешних сил на какую-либо ось за рассматриваемый промежуток времени равна нулю, то проекция количества движения механической системы на эту ось постоянна,
т.е.
если
 то
то .
.
Довольно часто удается выделить важные особенности движения механической системы, не прибегая к интегрированию системы дифференциальных уравнений движения. Это достигается применением общих теорем динамики.
5.1. Основные понятия и определения
Внешние и внутренние силы. Любая сила, действующая на точку механической системы, обязательно является либо активной силой, либо реакцией связи. Всю совокупность сил, действующих на точки системы, можно разделить на два класса иначе: на внешние силы и внутренние силы (индексы е и i - от латинских слов externus - внешний и internus - внутренний). Внешними называются силы, действующие на точки системы со стороны точек и тел, не входящих в состав рассматриваемой системы. Внутренними называются силы взаимодействия между точками и телами рассматриваемой системы.
Это разделение зависит от того, какие материальные точки и тела включены исследователем в рассматриваемую механическую систему. Если расширить состав системы, включив в нее дополнительно точки и тела, то некоторые силы, которые для прежней системы были внешними, для расширенной системы могут стать внутренними.
Свойства внутренних сил. Поскольку эти силы являются силами взаимодействия между частями системы, они входят в полную систему внутренних сил «двойками», организованными в соответствии с аксиомой действия-противодействия. У каждой такой «двойки» сил
главный вектор и главный момент относительно произвольного центра равны нулю. Так как полная система внутренних сил состоит только из «двоек», то
1) главный вектор системы внутренних сил равен нулю,
2) главный момент системы внутренних сил относительно произвольной точки равен нулю.
Массой системы называется арифметическая сумма масс тк всех точек и тел, образующих систему:
Центром масс (центром инерции) механической системы называется геометрическая точка С, радиус-вектор и координаты которой определяются формулами
где - радиусы-векторы и координаты точек, образующих систему.
Для твердого тела, находящегося в однородном поле тяжести, положения центра масс и центра тяжести совпадают, в других случаях это разные геометрические точки.
Вместе с инерциальной системой отсчета часто рассматривают одновременно неинерциальную систему отсчета, движущуюся поступательно. Ее оси координат (оси Кёнига) выбирают так, чтобы начало отсчета С постоянно совпадало с центром масс механической системы. В соответствии с определением центр масс неподвижен в осях Кёнига и находится в начале координат.
Моментом инерции системы относительно оси называется скалярная величина равная сумме произведений масс тк всех точек системы на квадраты их расстояний до оси:
![]()
Если механической системой является твердое тело, для нахождения 12 можно воспользоваться формулой

где - плотность, объем, занимаемый телом.
Теорема о движении центра масс. Дифференциальные уравнения движения механической системы. Теорема о движении центра масс механической системы. Закон сохранения движения центра масс.
Теорема об изменении количества движения. Количество движения материальной точки. Элементарный импульс силы. Импульс силы за конечный промежуток времени и его проекции на координатные оси. Теорема об изменении количества движения материальной точки в дифференциальной и конечной формах.
Количество движения механической системы; его выражение через массу системы и скорость ее центра масс. Теорема об изменении количества движения механической системы в дифференциальной и конечной формах. Закон сохранения количества движения механической
(Понятие о теле и точке переменной массы. Уравнение Мещерского. Формула Циолковского.)
Теорема об изменении момента количества движения. Момент количества движения материальной точки относительно центра и относительно оси. Теорема об изменении момента количества движения материальной точки. Центральная сила. Сохранение момента количества движения материальной точки в случае центральной силы. (Понятие о секторной скорости. Закон площадей.)
Главный момент количеств движения или кинетический момент механической системы относительно центра и относительно оси. Кинетический момент вращающегося твердого тела относительно оси вращения. Теорема об изменении кинетического момента механической системы. Закон сохранения кинетического момента механической системы. (Теорема об изменении кинетического момента механической системы в относительном движении по отношению к центру масс.)
Теорема об изменении кинетической энергии. Кинетическая энергия материальной точки. Элементарная работа силы; аналитическое выражение элементарной работы. Работа силы на конечном перемещении точки ее приложения. Работа силы тяжести, силы упругости и силы тяготения. Теорема об изменении кинетической энергии материальной точки в дифференциальной и конечной формах.
Кинетическая энергия механической системы. Формулы для вычисления кинетической энергии твердого тела при поступательном движении, при вращении вокруг неподвижной оси и в общем случае движения (в частности, при плоскопараллельном движении). Теорема об изменении кинетической энергии механической системы в дифференциальной и конечной формах. Равенство нулю суммы работ внутренних сил в твердом теле. Работа и мощность сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси.
Понятие о силовом поле. Потенциальное силовое поле и силовая функция. Выражение проекций силы через силовую функцию. Поверхности равного потенциала. Работа силы на конечном перемещении точки в потенциальном силовом поле. Потенциальная энергия. Примеры потенциальных силовых полей: однородное поле тяжести и поле тяготения. Закон сохранения механической энергии.
Динамика твердого тела. Дифференциальные уравнения поступательного движения твердого тела. Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси. Физический маятник. Дифференциальные уравнения плоского движения твердого тела.
Принцип Даламбера. Принцип Даламбера для материальной точки; сила инерции. Принцип Даламбера для механической системы. Приведение сил инерции точек твердого тела к центру; главный вектор и главный момент сил инерции.
(Определение динамических реакций подшипников при вращении твердого тела вокруг неподвижной оси. Случай, когда ось вращения является главной центральной осью инерции тела.)
Принцип возможных перемещений и общее уравнение динамики. Связи, налагаемые на механическую систему. Возможные (или виртуальные) перемещения материальной точки и механической системы. Число степеней свободы системы. Идеальные связи. Принцип возможных перемещений. Общее уравнение динамики.
Уравнения движения системы в обобщенных координатах (уравнения Лагранжа). Обобщенные координаты системы; обобщенные скорости. Выражение элементарной работы в обобщенных координатах. Обобщенные силы и их вычисление; случай сил, имеющих потенциал. Условия равновесия системы в обобщенных координатах. Дифференциальные уравнения движения системы в обобщенных координатах или уравнения Лагранжа 2-го рода. Уравнения Лагранжа в случае потенциальных сил; функция Лагранжа (кинетический потенциал).
Понятие об устойчивости равновесия. Малые свободные колебания механической системы с одной степенью свободы около положения устойчивого равновесия системы и их свойства.
Элементы теории удара. Явление удара. Ударная сила и ударный импульс. Действие ударной силы на материальную точку. Теорема об изменении количества движения механической системы при ударе. Прямой центральный удар тела о неподвижную поверхность; упругий и неупругий удары. Коэффициент восстановления при ударе и его опытное определение. Прямой центральный удар двух тел. Теорема Карно.
СПИСОК ЛИТЕРАТУРЫ
Основной
Бутенин Н. В., Лунц Я- Л., Меркин Д. Р. Курс теоретической механики. Т. 1, 2. М., 1985 и предыдущие издания.
Добронравов В. В., Никитин Н. Н. Курс теоретической механики. М., 1983.
Старжинский В. М. Теоретическая механика. М., 1980.
Тарг С. М. Краткий курс теоретической механики. М., 1986 и предыдущие издания.
Яблонский А. А., Никифорова В. М. Курс теоретической механики. Ч. 1. М., 1984 и предыдущие издания.
Яблонский А. А. Курс теоретической механики. Ч. 2. М., 1984 и предыдущие издания.
Мещерский И. В. Сборник задач по теоретической механике. М., 1986 и предыдущие издания.
Сборник задач по теоретической механике/Под ред. К. С. Колесникова. М., 1983.
Дополнительной
Бать М. И., Джанелидзе Г. Ю., Кельзон А. С. Теоретическая механика в примерах и задачах. Ч. 1, 2. М., 1984 и предыдущие издания.
Сборник задач по теоретической механике/5ражничен/со Н. А., Кан В. Л., Минцберг Б. Л. и др. М., 1987.
Новожилов И. В., Зацепин М. Ф. Типовые расчеты по теоретической механике на базе ЭВМ. М., 1986,
Сборник заданий для курсовых работ по теоретической механике /Под ред. А. А. Яблонского. М., 1985 и предыдущие издания (содержит примеры решения задач).



 материальных точек
материальных точек .Положение
каждой точки массой
.Положение
каждой точки массой определяется в инерциальной системе
отсчёта
определяется в инерциальной системе
отсчёта радиус-вектором
радиус-вектором (рис. 13.1).
Пусть
(рис. 13.1).
Пусть
 -
скорость точки
-
скорость точки .
.