Как найти высоту трапеции вписанной в окружность. Интересные свойства трапеции

Трапеция - это геометрическая фигура с четырмя углами. При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как "трапедзион", что означало "столик", "обеденный столик".

Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.

Элементы, виды и признаки геометрической фигуры трапеция

Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны - боковыми сторонами. При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.

У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:

1. Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.
2. При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
3. Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.
4. При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
5. При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
6. Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°. Отрезок, соединяющий основания, будет равен 1/2 их разности.

Свойства трапеции, описанной около окружности

Заключить окружность в трапецию возможно лишь при одном условии. Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.

Итак, подробнее о свойствах трапеции, описанной около окружности:

1. Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
2. При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
3. Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.

Еще немного о свойствах трапеции, заключенной в окружность

Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.

Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. Это значит, что при построении окружности, описанной около трапеции AFDM, применимо: AD × FM = AF × DM + FD × AM.

На школьных экзаменах довольно часто встречаются задачи, требующие решения задач с трапецией. Большое количество теорем необходимо запоминать, но если выучить сразу не получиться - не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.

- (греч. trapezion). 1) в геометрии четырехугольник, у которого две стороны параллельны, а две нет. 2) фигура, приспособленная для гимнастических упражнений. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТРАПЕЦИЯ… … Словарь иностранных слов русского языка

Трапеция - Трапеция. ТРАПЕЦИЯ (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту. … Иллюстрированный энциклопедический словарь

Четырехугольник, снаряд, перекладина Словарь русских синонимов. трапеция сущ., кол во синонимов: 3 перекладина (21) … Словарь синонимов

- (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту … Современная энциклопедия

- (от греч. trapezion букв. столик), четырехугольник, в котором две противоположные стороны, называемые основаниями трапеции, параллельны (на рисунке АD и ВС), а другие две непараллельны. Расстояние между основаниями называют высотой трапеции (на… … Большой Энциклопедический словарь

ТРАПЕЦИЯ, четырехугольная плоская фигура, в которой две противоположные стороны параллельны. Площадь трапеции равна полусумме параллельных сторон, умноженной на длину перпендикуляра между ними … Научно-технический энциклопедический словарь

ТРАПЕЦИЯ, трапеции, жен. (от греч. trapeza стол). 1. Четырехугольник с двумя параллельными и двумя непараллельными сторонами (мат.). 2. Гимнастический снаряд, состоящий из перекладины, подвешенной на двух веревках (спорт.). Акробатические… … Толковый словарь Ушакова

ТРАПЕЦИЯ, и, жен. 1. Четырёхугольник с двумя параллельными и двумя непараллельными сторонами. Основания трапеции (её параллельные стороны). 2. Цирковой или гимнастический снаряд перекладина, подвешенная на двух тросах. Толковый словарь Ожегова. С … Толковый словарь Ожегова

Жен., геом. четвероугольник с неравными сторонами, из коих две опостенны (паралельны). Трапецоид, подобный четвероугольник, у которого все стороны идут врознь. Трапецоэдр, тело, ограненное трапециями. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля

- (Trapeze), США, 1956, 105 мин. Мелодрама. Начинающий акробат Тино Орсини поступает в цирковую труппу, где работает Майк Риббл, известный в прошлом воздушный гимнаст. Когда то Майк выступал вместе с отцом Тино. Молодой Орсини хочет, чтобы Майк… … Энциклопедия кино

Четырехугольник, две стороны которого параллельны, а дведругие стороны не параллельны. Расстояние между параллельными сторонаминаз. высотою Т. Если параллельные стороны и высота содержат а, b и hметров, то площадь Т. содержит квадратных метров … Энциклопедия Брокгауза и Ефрона

1. Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
2. Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения - подобны
3. Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции - равновеликие (имеют одинаковую площадь)
4. Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
5. Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
6. Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b - основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .

Данный отрезок параллелен основаниям трапеции .

Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD - BC)/2
или
LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции - являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными - они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).

Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.

Что из этого следует?

Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это - треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.

Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .

Таким образом, любая трапеция может быть достроена до треугольника. При этом:

• Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
• Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).

KO / ON = BC / AD

Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:

• Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
• Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Формулы для нахождения диагоналей трапеции

a, b - основания трапеции

c, d - боковые стороны трапеции

d1 d2 - диагонали трапеции

α β - углы при большем основании трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:

1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований . Данное свойство диагоналей трапеции может быть доказано как отдельная теорема

2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.

3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ

Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.

Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.

Формулы нахождения диагоналей трапеции через высоту

Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.

Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

Треугольники AOD и BOC являются подобными по трем углам - AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.

Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть

AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16

Ответ : 16 см

Задача .
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.

Решение .
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая - то обозначим длину AM = a, длину KD = b (не путать с обозначениями в формуле нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK - прямоугольник.

Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 - b

Треугольники DBM и ACK - прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора

H 2 + (24 - a) 2 = (5√17) 2
и
h 2 + (24 - b) 2 = 13 2

Учтем, что a = 16 - b , тогда в первом уравнении
h 2 + (24 - 16 + b) 2 = 425
h 2 = 425 - (8 + b) 2

Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 - (8 + b) 2 + (24 - b) 2 = 169
-(64 + 16b + b) 2 + (24 - b) 2 = -256
-64 - 16b - b 2 + 576 - 48b + b 2 = -256
-64b = -768
b = 12

Таким образом, KD = 12
Откуда
h 2 = 425 - (8 + b) 2 = 425 - (8 + 12) 2 = 25
h = 5

Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b - основания трапеции, h - высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2

Ответ : площадь трапеции равна 80 см 2 .

Проектная работа « Интересные свойства трапеции » Выполнили: ученицы 10 класса Кудзаева Эллина Баззаева Диана МКОУ СОШ с. Н.Батако Руководитель: Гагиева А.О. 20.11.2015 года

Цель работы: Рассмотреть свойства трапеции, которые в школьном курсе геометрии не изучаются, но при решении геометрических задач ЕГЭ из развернутой части С 4 бывает необходимо знать и уметь применять именно эти свойства.

Свойства трапеции: Если трапеция разделена прямой, параллельной ее основаниям, равным a и в, на две равновеликие трапеции. Тогда отрезок к этой прямой, заключенный между боковыми сторонами, равен a В к

Свойство отрезка, проходящего через точку пересечения диагоналей трапеции. Отрезок, параллельный основаниям, проходящий через точку пересечения диагоналей равен: а в с

Свойства трапеции: Отрезок прямой, параллельной основаниям трапеции, заключенный внутри трапеции, разбивается ее диагоналями на три части. Тогда отрезки, прилегающие к боковым сторонам, равны между собой. МР=ОК Р М О К

Свойства равнобедренной трапеции: Если в трапецию можно вписать окружность, то радиус окружности есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону. О С В А Д. Е О

Свойства равнобедренной трапеции: Если центр описанной окружности лежит на основании трапеции, то её диагональ перпендикулярна боковой стороне О А В С Д

Свойства равнобедренной трапеции: В равнобедренную трапецию можно вписать окружность, если боковая сторона равна её средней линии. С В А Д h

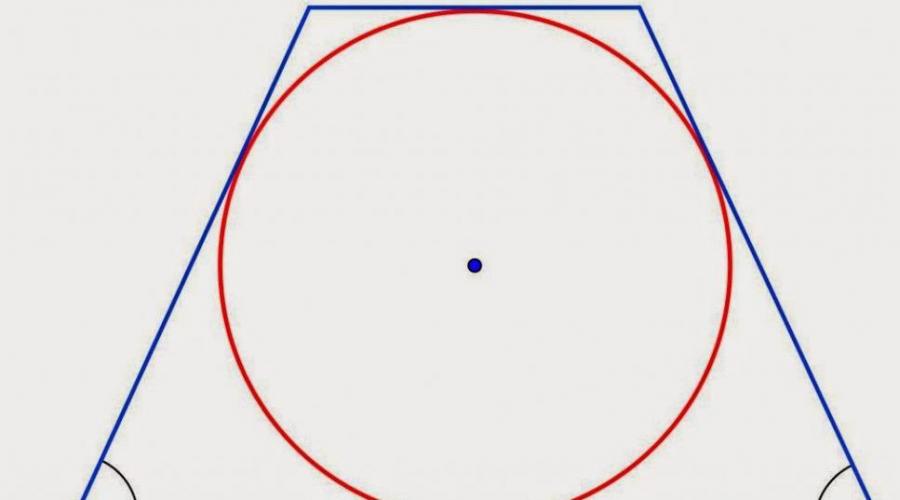
1)Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства: 1. Сумма оснований трапеции равна сумме боковых сторон. 2. Расстояния от вершины трапеции до точек касания вписанной окружности равны. 3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности. 4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции. 5. Если точка касания делит боковую сторону на отрезки m и n , то радиус вписанной окружности равен

Свойства прямоугольной трапеции, в которую вписана окружность: 1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции - квадрат, сторона которого равна радиусу. (AMOE и BKOM - квадраты со стороной r). 2) Если в прямоугольную трапецию вписана окружность, то площадь трапеции равна произведению ее оснований: S=AD*BC

Доказательство: Площадь трапеции равна произведению полусуммы ее оснований на высоту: Обозначим CF=m , FD=n . Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а

I. Биссектрисы углов при боковой стороне трапеции пересекаются под углом 90º . 1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB). 2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам). 3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º. Вывод: Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом. Это утверждение применяется при решении задач на трапецию, в которую вписана окружность.

I I .Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции. Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS - равнобедренный с основанием BS Значит, его биссектриса AK является также медианой, то есть точка K - середина BS. Если M и N - середины боковых сторон трапеции, то MN - средняя линия трапеции и MN∥AD. Так как M и K - середины AB и BS, то MK - средняя линия треугольника ABS и MK∥AS. Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.

III. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABK и DCK - равнобедренные с основаниями AK и DK соответственно. Таким образом, BC=BK+KC=AB+CD. Вывод: Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.

I V. Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию. В этом случае треугольники ABF и DCF - равнобедренные с основаниями BF и CF соответственно. Отсюда AD=AF+FD=AB+CD. Вывод: Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции. У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.

Если равнобедеренную трапецию со сторонами а,в,с, d можно вписать и около неё можно описать окружности, то площадь трапеции равна

Добрый вечер! Ох уж эти описанные, или вписанные окружности, геометрические фигуры. Так сложно запутаться. что да когда.

Давайте попробуем разобраться для начала с формулировкой. Нам дана окружность описанная около . Иными словами — данная трапеция вписана в окружность.

Давайте вспомним, что описать окружность мы можем только вокруг . А равнобедренная трапеция в свою очередь — это трапеция, у которой боковые стороны равны.

Давайте попробуем решить задачку. Нам известно, что основания равнобедренной трапеции ADCB равны 6 (DC) и 4 (AB). А радиус описанной окружности равен 4. Нужно найдите высоту трапеции FK.

FK — высота трапеции. её нам нужно найти, но перед этим вспомним, что точка О — это центр окружности. А ОС, ОD, OA, OB — известные радиусы .

В OFC нам известна гипотенуза, которая является радиусом окружности, а катет FC = половине основания DC = 3 см (так как DF = FC).

Теперь по найдём OF:

А в прямоугольном треугольнике OKB нам тоже известна гипотенуза, так как это радиус окружности. А KB равняется половине AB; KB = 2 см. И, используя теорему Пифагора вычислим отрезок OK: